Зачёт кое-как сдал, а всё равно толком не понял?
Работа сделана по учебнику "Алгебра и начала математического анализа. 10 класс" Никольского и других
Что такое факториал? Это такое число. Оно является характеристикой другого числа. Но не любого числа, а натурального или числа 0. А какие числа являются натуральными? Это 1, 2, 3, 4, 5, 6, 7 и так далее. Обозначается факториал восклицательным знаком. Например, факториал числа 3 пишется так: 3! Факториал числа 0 равен 1 (запишем это так 0!=1). Так условились математики. Как вычисляется факториал других чисел? Вычислим, например, факториал числа 5. Для этого 1 умножим на 2, затем на 3, затем на 4, и затем на 5 . Получается у нас 120 Запишем: 5!=120. Как вычисляется факториал других чисел, смотрите на рисунке 1. Вы поняли закономерность?
Попробуйте сформулировать правило: Чтобы вычислить факториал числа, нужно:
Нужно перемножить все натуральные числа, которые меньше, чем это число, между собой и умножить на это число. Можно ещё проще сформулировать: нужно умножить на число все натуральные числа, которые меньше, чем это число.
Замечание: Обратите внимание, что факториал числа равен факториалу числа, меньшего на 1, умноженному на это (большее) число. (n+1)!=(n+1)n!
А зачем нужно знать этот факториал? Об этом дальше. Допустим, у нас есть набор из двух элементов: x1 и x2 . Вопрос: сколькими способами их можно расположить? Ответ: двумя. Первый способ: x1 на первом месте, x2 на втором. Второй способ: x2 на первом месте, x1 на втором.
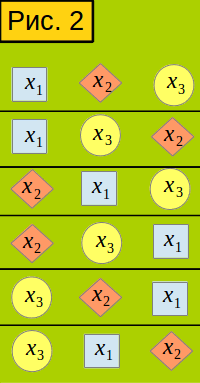
Допустим, у нас набор из трёх элементов: x1, x2, x3 . Сколькими способами можно их расположить? Все возможные варианты на рис. 2. Всего вариантов 6. Каждый такой вариант называется перестановкой
Докажем, что число возможных перестановок набора из n элементов равно n!, то есть факториал n . Будем доказывать методом математической индукции.
Предположим, у нас есть какое - то выражение с переменной n . Нам надо доказать, что при n, равном любому натуральному числу (то есть 1, 2, 3, 4 и так далее) выражение будет верным. Мы можем воспользоваться методом доказательства, который называется методом математической индукции. Состоит этот метод из трёх шагов. Никакой из этих шагов нельзя пропускать.
Шаг 1. Нужно доказать, что если n=1 то выражение будет верным.
Шаг 2. Нужно предположить, что при n равном какому - то произвольному натуральному числу k выражение будет верным. Запишем это так: n=k , выражение верное. Уточню: здесь не следует подставлять вместо n какое - то конкретное число.
Шаг 3. Нужно доказать, что если n=k+1 выражение будет верным.
Попробуйте доказать, что если вы правильно проделали все три шага, выражение будет верным при любом натуральном n .
Предположим, n у нас равно 1. Мы уже доказали, что в этом случае выражение будет верным. Но тогда, согласно шагу три при n=1+1=2 выражение тоже будет верным. Но тогда при n=2+1=3 выражение тоже будет верным. Но тогда при n=3+1 выражение тоже верное. Аналогично мы можем доказать верность выражения для любого натурального числа.
Допустим, мы доказали методом математической индукции, что при n равном любому натуральному числу выражение будет верным. Можно ли считать доказанным, что выражение будет верным при n=3,5 ?
3,5 не является натуральным числом. Поэтому считать выражение доказанным при n=3,5 нельзя.
Вернёмся к перестановкам. Число возможных перестановок (вариантов расположения) набора из n элементов обозначают как Pn От слова Perestanovka (шутка). Итак, доказываем методом математической индукции, что число возможных перестановок набора из n элементов равно n! (факториалу n). Pn=n!
Делаем первый шаг. При n=1 число возможных перестановок равно 1 Факториал числа 1 тоже равен 1 Поэтому P1=1!
Делаем второй шаг. Предположим, что n=k и число перестановок при этом равно k! (факториалу k) Pn=k! Смотрим рис. 3, позиция 1. В розовом прямоугольнике я изобразил возможные перестановки набора из k элементов. Для простоты я не стал рисовать их все.
Делаем третий шаг. Докажем, что при n=k+1 число перестановок равно (k+1)! Pk+1=(k+1)! Смотрим рис. 3, позиция 2. Сделаем из набора из k элементов набор из (k+1) элементов. Добавим к нему жёлтую звёздочку. Звёздочка может быть расположена на первом месте (верхняя строчка), на втором (строчка ниже), на третьем, .... и так, вплоть до последнего места. Всего вариантов расположения звёздочки k+1 (перед каждым из k элементов, и на последнем месте). При каждом из вариантов расположения звёздочки возможны k! перестановок остальных элементов (согласно шагу 2). Поэтому число возможных перестановок набора из k+1 элементов равно (k+1)k! Это выражение, согласно замечанию к определению факториала (приведено выше) равно (k+1)! (факториалу (k+1)).
Pk+1=(k+1)Pk=(k+1)k!=(k+1)!
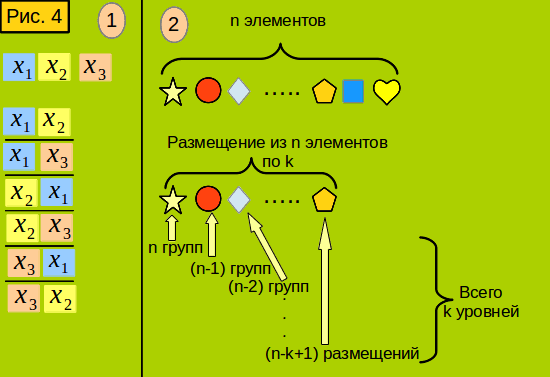
Смотрим рис. 4, позиция 1. Даны три элемента: x1 x2 x3. Из них можно составить различные пары, отличающиеся друг от друга либо составом элементов, либо порядком их следования. Всего возможных пар 6. Такие пары называют упорядоченными наборами из 2 элементов, составленными из 3 элементов. Пусть даны n элементов. Из них можно составить различные упорядоченные наборы из k элементов, отличающиеся друг от друга либо составом элементов, либо порядком их следования. Такие наборы также называют размещениями из n элементов по k. Количество возможных размещений обозначают как Akn. A1n=n , то есть число возможных размещений из n элементов по 1 равно n, что очевидно. Чему равно число возможных размещений из n элементов по 2? Снова смотрим рис. 4, поз. 1. Все размещения можно разделить на группы: начинающиеся с x1, x2, x3. Количество таких групп равно числу элементов, то есть трём. В каждой группе размещения различаются вторым элементом. Рассмотрим верхнюю группу, где первый элемент x1 (голубой). На второй позиции голубой уже быть не может, там может быть только либо x2 (жёлтый), либо x3 (бежевый). Поэтому число размещений в группе равно двум, то есть 3-1. Общее число размещений равно 3(3-1)=6
Теперь найдём общее решение задачи. Смотрим рис. 4, позиция 2. Дано n элементов. Найдём, сколько из них можно составить размещений по k элементов. Если k больше 1, все размещения можно разделить на группы, начинающиеся с каждого из элементов: звёздочки, кружка, ромба ... Всего групп n. Назовём их группами первого уровня. Если k больше 2, тогда каждую группу первого уровня в свою очередь тоже можно разделить на группы, по элементу, находящемуся на втором месте. На втором месте уже не может находиться элемент, который находится на первом месте. Поэтому всего таких групп n-1. Назовём их группами второго уровня. Если k больше 3, тогда группы второго уровня, в свою очередь, тоже можно разделить на группы, по элементу, находящемуся на третьем месте. На третьем месте уже не могут находиться элементы, находящиеся на первых двух местах. Поэтому всего таких групп n-2. Назовём их группами третьего уровня. На последнем уровне находятся не группы размещений, а размещения, число их равно (n-k+1) . Общее число уровней равно k . Поэтому число множителей уравнения равно k. Общее число размещений равно Akn=n(n-1)....(n-k+1)
Чему будет равно число размещений, если k=n ?
В этом случае размещение является перестановкой из n элементов. Их возможное число равно n! Вы также можете получить этот результат и из выше приведённой формулы.
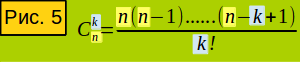
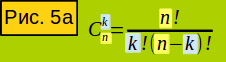
Снова посмотрите рис. 4 позиция 1. На нём изображены все возможные размещения из трёх элементов по два. Каждому из размещений можно подобрать другое, с таким же составом элементов, но с иным их расположением. Первому сверху соответствует третье сверху, второму - пятое, четвёртому - шестое. Такие размещения с одинаковым составом элементов считаются одним сочетанием элементов. Таким образом, на рисунке изображено шесть размещений, но три сочетания из трёх элементов по два. Обозначаются сочетания большой буквой C (от слова Combination). Сочетание из n элементов по k записывается так: Сkn. То есть в нём k элементов, которые являются членами большего набора из n элементов. Как вычислить число возможных сочетаний в наборе из n элементов по k ? Сделать это легко. Выше мы вывели формулу вычисления числа возможных размещений в таком наборе. Все размещения в наборе из n элементов по k входят в группы с одинаковым составом элементов, но с различным их расположением, то есть с различными перестановками. Каждая такая группа является сочетанием из n элементов по k. Число возможных перестановок в ней равно k! (это мы доказали в разделе про перестановки). Чтобы вычислить число возможных сочетаний в наборе из n элементов по k, нужно число возможных размещений разделить на k! Формула на рис. 5. Эту формулу можно преобразовать в более компактную (рис. 5а).
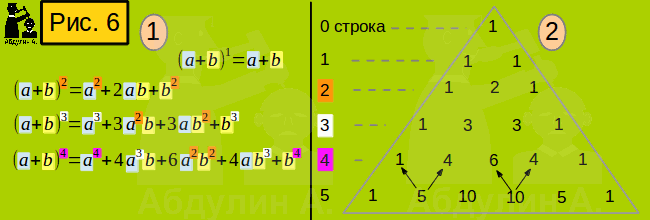
Смотрим рисунок 6 позиция 1. Приведены четыре формулы. Попытайтесь мысленно выделить все закономерности, которые присутствуют во всех четырёх формулах. Попробуем выразить правило их создания. Чему равно выражение (a+b)n ? Оно равно сумме членов an, an-1b, an-2b2 ...., abn-1, bn с определёнными числовыми коэффициентами. Обратите внимание: с каждым последующим членом степень a убывает на единицу, в первом члене она равна n, а в предпоследнем члене она равна 1. Степень b, наоборот, с каждым последующим членом прибывает на единицу. Во втором члене она равна 1, а в последнем члене она равна n. Всего членов столько, чтобы эти правила соблюдались, а именно n+1 .
Что касается числовых коэффициентов, то их можно вычислить с помощью "треугольника Паскаля". Он изображён на рис. 6 позиция 2. Устроен он так: на нулевой, самой верхней строке стоит 1. Номер каждой следующей строки соответствует n. То есть числовые коэффициенты формулы выражения (a+b)n находятся на n строке. Во второй строке находятся две единицы. В последующих строках на первом и последнем месте находятся единицы. Остальные n-1 внутренних чисел в каждой строке вычисляются так: каждое внутреннее число равно сумме двух чисел, которые находятся над ним (двух ближайших). Для двух чисел я стрелками показал, суммой каких чисел они являются. Обратите внимание, как изменяются числа в каждой строчке треугольника.
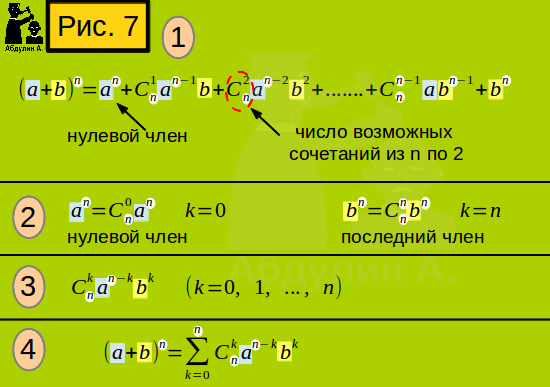
Для больших n рисовать такой треугольник было бы слишком трудоёмко. Поэтому также испольуется формула, называемая биномом Ньютона. Она на рис. 7, позиция 1. Как с каждым последующим членом изменяется степень a (от n до 1) и b (от 1 до 0), я уже объяснял выше. Число членов, как было сказано выше, равно n+1 . Осталось объяснить, что в формуле означает Cnk . А означает это тот самый числовой коэффициент, который мы находили при помощи треугольника Паскаля. Эти коэффициенты ещё называют биномиальными коэффициентами. an считается нулевым членом. Его биномиальный коэффициент равен 1, хотя это не очевидно (сколько может быть сочетаний по 0 элементов, интересный вопрос!). Биномиальный коэффициент последнего члена (bn) равен 1 . У других членов он равен числу возможных сочетаний из n по k, где во первом (не путать с нулевым) члене k=1, во втором члене k=2, в предпоследнем члене k=n-1 . Биномиальный коэффициент нулевого и последнего члена можно выразить через Cnk Смотрите рис. 7, позиция 2. Тогда каждый член выражения можно выразить так: смотрите рис. 7, позиция 3. Формулу можно записать так: смотрите рис. 7, позиция 4. Выразим правую часть формулы (рис. 7.4) словами: сумма слагаемых (формула слагаемого на позиции 3), взятая для всех целых k от 0 до n . Доказательство треугольника Паскаля и бинома Ньютона приводить не буду, так как они весьма громоздкие.
Допустим, у нас есть игральный кубик, на гранях которого отмечены очки, от одного до шести. Произведём научный опыт: бросим этот кубик. Когда он перестанет кувыркаться, одна из граней окажется наверху. Если наверху окажется грань с одним очком, назовём это событием A1, если с двумя - событием A2, с тремя - A3 и так далее. Допустим, кубик из однородного материала, и нет оснований предпологать, что вероятность того, что наверху окажется какая-либо из граней, больше вероятности, что наверху окажется какая то другая грань. События A1,A2,A3,A4,A5,A6 являются равновозможными.
Как бы мы не бросили кубик, какая то из граней всё равно окажется наверху. Говоря математическим языком, события A1,A2,A3,A4,A5,A6 являются единственно возможными. То есть в любом опыте: 1. Обязательно произойдёт одно и только одно из этих событий. 2. Других событий быть не может. Такие события, которые являются и равновозможными, и единственно возможными, будем также называть случаями.
Вот вам ещё неколько терминов. Если в результате опыта событие обязательно произойдёт, его называют достоверным. Если мы будем считать одним событием (случаем) выпадание любой из граней, это событие будет достоверным. Если в опыте событие произойти не может, его называют невозможным. Например, в нашем опыте является невозможным выпадание семи очков. В кубике нет такой грани. События (два или более) называют несовместными, если в опыте они не могут произойти одновременно, или, говоря другими словами, одно событие исключает другое (или другие). Отметим, что если события единственно возможны, то они и несовместны.
почему?
если события единственно возможны, то может произойти только одно из них, и это событие исключает другие
а если события несовместны, означает ли это, что они единственно возможны?
нет
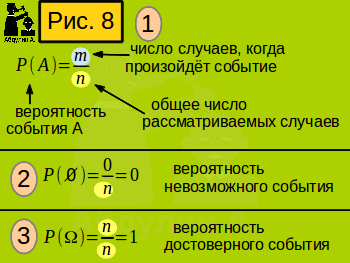
Вот ещё термин: вероятность события. Это отношение случаев, когда это событие произойдёт, к общему числу рассматриваемых случаев. Как записывается вероятность события, смотрите на рисунке 8. Обратите внимание на знаки, которыми обозначается невозможное событие и достоверное событие. Вероятность невозможного события, естественно, равна нулю, а вероятность достоверного события равна единице.
Суммой (объединением) событий A и B называют событие, когда происходит либо событие A, либо событие B, либо они оба вместе.
Если происходят оба события, то они не являются .....
несовместными
Сумму событий обозначают так: смотрите рисунок 9, позиция 1. Если события A и B несовместные, то их сумму будем обозначать по другому: A+B . Сумму n несовместных событий будем обозначать так: A1+A2+.....+An
Произведением (пересечением) событий A и B называют событие, когда происходят оба события, и A, и B . Произведение событий A и B обозначают либо как на рис. 9, поз. 2, либо просто AB . Здесь смысл слов "сумма" и "произведение" отличен от того, к которому мы привыкли.
Вероятности событий обладают следующими свойствами:
Вот вам ещё термин: если единственно возможных событий два, их называют противоположными. Например, выпадание у кубика чётного числа очков и нечётного числа очков являются противоположными событиями. Выпадание у подброшенной монеты "орла" или "решки" - тоже противоположные события. Событие, противоположное событию A, обозначают той же буквой A, но с чёрточкой сверху (рис. 9, поз. 6 )
Противоположные события являются ...термин..? Их сумма есть ..термин..?
Противоположные события являются несовместными. Их сумма есть достоверное событие. Вероятность его равна 1.
Если события A и B несовместны, чему равна вероятность их произведения P(AB)?
вероятность произведения несовместных событий A и B равна нулю: P(AB)=0
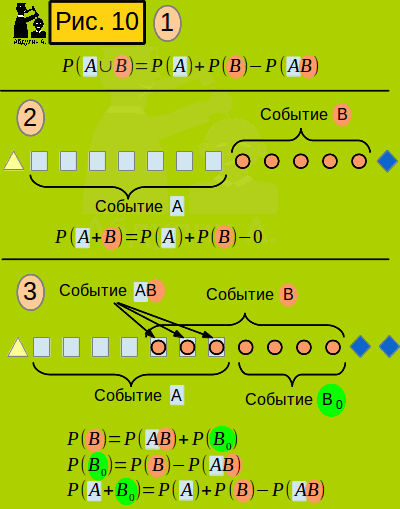
А зачем вам нужно знать вот это всё? На рис. 10, позиция 1 формула, которая может иметь практическое применение. Расшифруем формулу: вероятность суммы двух событий (того, что произойдёт хотя бы одно из событий) равна сумме вероятностей этих событий минус вероятность произведения этих событий (того, что в одном случае произойдут оба события).
Докажем формулу. Смотрим рис. 10, поз. 2. Допустим, два события являются несовместными. Тогда вероятность их суммы равна сумме их вероятностей (рис. 9, поз. 5). Вероятность их произведения равна нулю (по определению несовместности и определению произведения событий). Формула для двух несовместных событий верна. Теперь рассмотрим случай, когда два события не являются несовместными (то есть они оба могут произойти в одном случае). Смотрим рис. 10, поз. 3. Событие B можно представить как сумму двух несовместных событий: AB и B0. Значит, вероятность события B равна сумме вероятностей этих событий (позиция 3, верхняя формула). Далее вычисляем вероятность события B0 (позиция 3, средняя формула). Событие A+B можно представить как сумму двух несовместных событий - A и B0. Вероятность события A+B равна сумме вероятностей этих несовместных событий (поз. 3, нижняя формула). Формула доказана.
Приведу пример из учебника по математике за 10 класс Никольского и др. Два математика, Бюффон и Пирсон, много раз бросали монету и записывали, когда выпадет герб. Вот результат их опытов.
| Число бросаний | Число выпаданий герба | Относительная частота выпаданий герба | |
|---|---|---|---|
| Бюффон | 4040 | 2048 | 0,5085 |
| Пирсон | 12000 | 6019 | 0,5046 |
| Пирсон | 14000 | 12012 | 0,5005 |
Вопрос: что они измеряли? Они измеряли отношение числа событий, то есть выпаданий герба (мы обозначим его буквой m) к числу опытов (обозначим его буквой n). Отношение m/n называют относительной частотой события. А вот я выше давал определение вероятности (рис. 8, поз. 1). Сейчас напрягите мозги, прежде чем кликать по вопросу.
В чём разница между понятиями "относительная частота события" и "вероятность события"?
Вероятность события вычисляется теоретически, при этом рассматриваются возможные случаи одного опыта. Относительная частота события измеряется практически, при этом производится большое количество опытов.
Практика показывает, однако, что при большом количестве опытов относительная частота события, как правило, мало отличается от вероятности. И чем больше количество опытов, тем их значения ближе. Часто не удаётся вычислить вероятность события. Тогда при достаточном числе опытов относительная частота события может рассматриваться как приближённое значение вероятности.
Пусть производится несколько независимых опытов. Опыты называют независимыми, если результат в каждом из них не зависит от результата в других опытах. Такие серии опытов называют сложным опытом. Есть много задач, где нужно определить вероятность определённого сочетания результатов в сложном опыте. Например, пусть производится сложный опыт, состоящий в том, что сначала подбрасывается монета, а затем бросается кубик. Нам нужно узнать вероятность того, что в первом опыте сложного опыта выпадет герб (назовём это событием A), а во втором опыте этого же сложного опыта у кубика выпадет 3 очка (назовём это событием B). Вероятность, что в первом опыте выпадет герб, равна 1/2 (P(A)=1/2), вероятность, что во втором опыте выпадет 3 очка, равна 1/6 (P(B)=1/6). Вероятность же сочетания этих событий равна (1/2)(1/6)=1/12.
P(A, B)=P(A)P(B)
Эта формула обобщается и на n независимых опытов:
P( A1, A2,..., An)= P(A1)P(A2)....P(An) .
Например, бросают монету 4 раза, и нужно узнать вероятность того, что все 4 раза выпадет герб. Вероятность, что в каждом отдельном опыте выпадет герб, равна 1/2. (1/2)(1/2)(1/2)(1/2)=(1/2)4=1/16
Пусть в опыте (назовём его простым) вероятность события A равна p. Производится сложный опыт, состоящий из n простых опытов. Результат в каждом простом опыте не зависит от результата других простых опытов. Тогда в сложном опыте вероятность события Ak, заключающегося в том, что событие A происходит k раз (k не больше n), равна (внимательно и не спеша изучаем формулу на рис. 11). Обратите внимание, что обычно вместо Pn(An) пишут Pn(k). Формулу на рис. 11 называют формулой Бернулли.
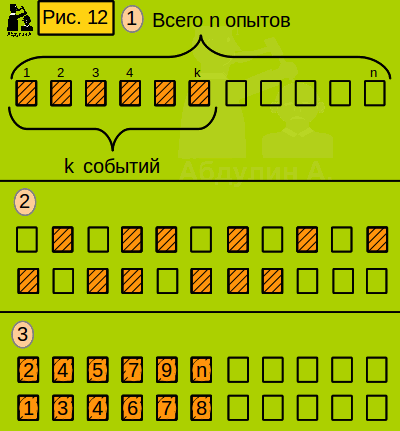
Теперь разжёвываю. Смотрим рис. 12, поз. 1 Я изобразил один из возможных результатов такого сложного опыта. Сначала происходят k событий A, а затем событие A не происходит. Какова вероятность именно такого результата сложного опыта? Вероятность того, что событие А произойдёт k раз подряд, равна pk. Кому непонятно, читайте предыдущий раздел "Сложный опыт". В каждом простом опыте вероятность того, что событие A не произойдёт, равна 1-p (в формуле мы присвоили это значение переменной q). Количество случаев, когда событие A не произошло, равно n-k . Вероятность таких случаев равна qn-k. Поэтому вероятность результата сложного опыта, что на рис. 12, поз 1 равна pk qn-k
Но это вероятность только одного результата сложного опыта. А ведь возможны и другие результаты, когда события A произошли в других простых опытах, но количество событий A в сложном опыте также равно k. Некоторые я изобразил на рис. 12, поз. 2 Вероятность каждого такого результата такая же, как и того, что мы разбирали. Поэтому нам надо найти число возможных результатов сложного опыта.
Выше в этой работе есть раздел про сочетания. Перечитайте его, если подзабыли. Число результатов равно числу сочетаний из n по k. Для наглядности я изобразил некоторые из возможных сочетаний на рис. 12 поз. 3. Это те же сочетания, что на позиции 2.
Умножаем число возможных результатов на вероятность каждого результата. Получаем формулу на рис. 11.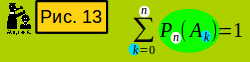
Гляньте на формулу на рис 13. Она выражает первое свойство чисел Pn(k): для любого натурального n сумма всех чисел Pn(k) равна 1. Для тех, кто не понял, объясняю популярно. В сложном опыте, состоящем из n простых опытов событие может произойти k раз, где k может принимать значения от 0 до n. Если сложить вероятности, что событие произойдёт k раз, для кажого из возможных значений k (от 0 до n), получится единица. Если вдуматься, это становится очевидным. Единица - вероятность достоверного события, в нашем случае сложного опыта.
Перед тем, как разъяснять второе свойство чисел Pn(k), приведу два примера из учебника Никольского. В таблице приведены приближённые значения P10(k) для p=1/5 Для тех, кто не понял: p - это вероятность события в простом опыте, k - число таких событий в сложном опыте, P10(k) - это вероятность, что в сложном опыте из 10 простых опытов событие произойдёт k раз.
| k | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| P10(k) | 0,1074 | 0,2684 | 0,3020 | 0,2013 | 0,0880 | 0,0264 |
Вот второй пример. В таблице приведены значения P6(k) для p=2/3 Кому непонятно, читайте объяснения к предыдущему примеру.
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| P6(k) | 0,0014 | 0,0165 | 0,0823 | 0,2195 | 0,3292 | 0,2633 | 0,0878 |
В обоих таблицах значение Pn(k) возрастает, достигает максимума, потом снова идёт на спад. Значение k , при котором Pn(k) максмиальна, приблизительно равно np, иногда np+1 . В первом примере np=10(1/5)=2 . Соответвенно Pn(k) максимальна при k=2 . Во втором примере np=6(2/3)=4 . Соответвенно Pn(k) максимальна при k=4 . Обратите внимание, что по краям таблиц, при минимальном и максимальном k, значения Pn(k) невелики. Наибольшие значения Pn(k) группируются вокруг максимального. Вот эти закономерности и составляют второе свойство чисел Pn(k) . Для тех, кому непонятно, разжёвываю: Допустим, вероятность события в простом опыте равна p. Производится сложный опыт, соотоящий из n простых опытов. Тогда максимальна вероятность, что в этом сложном опыте событие произойдёт np раз (в некоторых случаях np+1 раз). Велика вероятность, что событие произойдёт np+1 раз или np-1 раз. Вероятность, что событие произойдёт другое число раз, гораздо меньше, и чем больше это число отличается от np, тем меньше. В учебнике Никольского приводятся в обоснование этой закономерности математические выкладки. Кому интересно, сами скачивайте и вникайте.
Далее привожу цитату из Никольского: "Эти примеры подтверждают так называемый закон больших чисел. Пусть в опыте вероятность некоторого события A равна p. Тогда при многократном повторении опыта (считая эти опыты независимыми) близка к 1 вероятность того, что относительная частота события A (то есть отношение числа событий к числу опытов) мало отличается от p". Учебник приводит и более строгую формулировку закона. Кому интересно, читайте там.
Об ошибках сообщайте по адресу obuchmat@mail.ru
наверх