Зачёт кое-как сдал, а всё равно толком не понял?


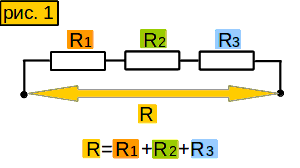
Просто, как ..... Сложил все эти сопротивления и получил сопротивление цепи.
Рассмотрим участок с двумя параллельными одинаковыми сопротивлениями. Сопротивление его в два раза меньше, чем каждого сопротивления. Если сопротивлений три, сопротивление участка будет в три раза меньше.
Какую тут можно провести аналогию?
Несколько одинаковых дырок. Через них протечёт воды в столько раз больше, чем через одну дырку, сколько дырок имеется.
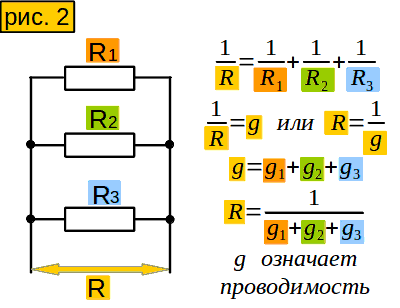
А как быть, если сопротивления не одинаковые? Есть такое понятие - проводимость. Оно означает величину, обратную сопротивлению. (рисунок 2)
Так если сопротивление больше, то проводимость что?
меньше
Чтобы вычислить проводимость нашего участка, надо сложить проводимости сопротивлений. Потом можно легко найти сопротивление участка.
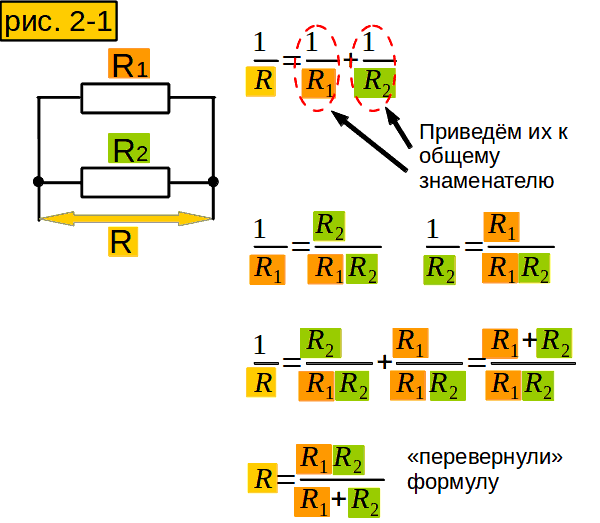
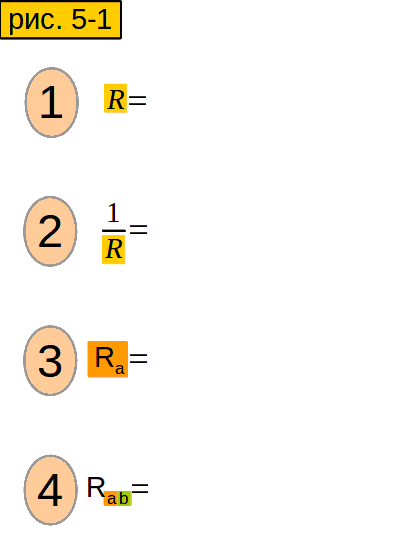
А нельзя ли вычислить сопротивление участка, не преобразуя сопротивления в проводимости, а потом обратно? Можно. Пусть у нас участок из двух параллельно соединённых сопротивлений (рис. 2-1). Проводимость его равна сумме проводимостей сопротивлений (1 строчка). Приведём проводимости сопротивлений к общему знаменателю (2 строчка). Сложим их и получим суммарную проводимость (3 строчка). "Переворачиваем" формулу (4 строчка) и получаем формулу для участка из двух параллельно соединённых сопротивлений. А если сопротивлений не два, а больше?
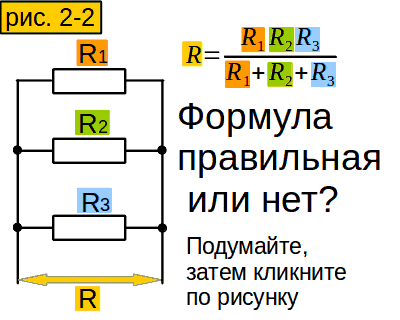

Сформулируйте своими словами формулу сопротивления участка из нескольких параллельных сопротивлений, чтобы лучше её запомнить.
Надо умножить все сопротивления, и разделить на сумму произведений этих сопротивлений, но в каждом этом произведнии одного сопротивления не хватает. Вы, может быть, и получше сформулируете.
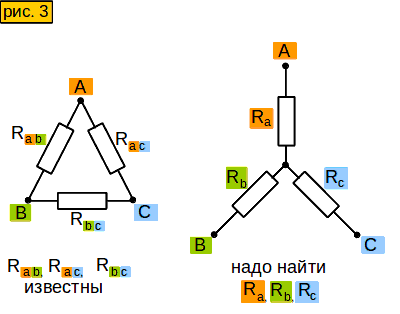
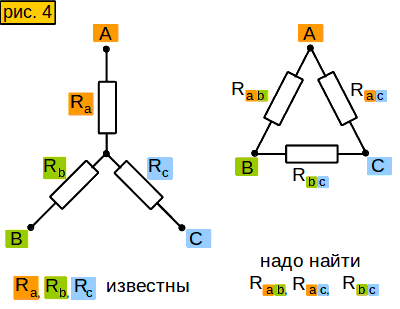
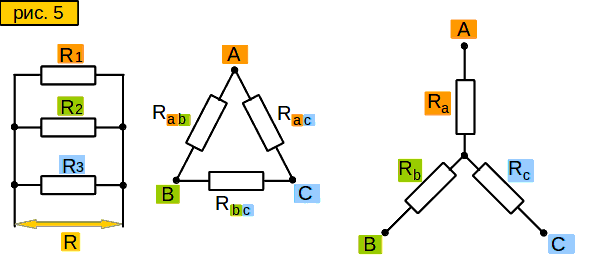
Пусть у нас в схеме есть вот такой участок цепи - "треугольник" (рис. 3, слева). Нам надо заменить его участком вот такого вида - "звездой" (рис. 3, справа), но чтобы сопротивления между сторонами "звезды" были такими же, как между соответствующими лучами "треугольника". Зачем это нужно? Позже узнаете.
Смотрим на "звезду" на рис. 3. Допустим, мы знаем сопротивления между точками A и B, то есть (Ra+Rb); A и C, то есть (Ra+Rc); B и C, то есть (Rb+Rc). Чему будут равны сопротивления Ra, Rb, Rc ?
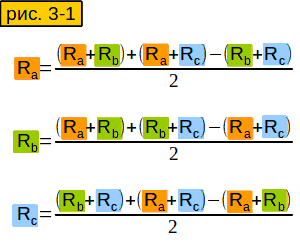
Зная все сопротивления между концами лучей "звезды", мы можем вычислить сопротивление каждого отдельного луча.
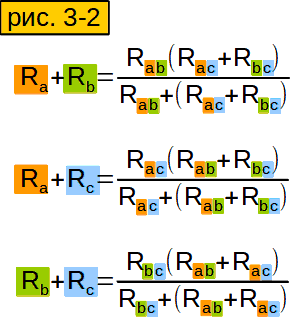
Теперь будем вычислять сопротивления между точками A, B, и C (звезды) через сопротивления треугольника, которые нам известны (рис. 3-2). Для начала вычислим сопротивление между точками A и B звезды (рис. 3-2 верхняя строчка). В нашем треугольнике мы имеем два параллельно включённых сопротивления - Rab и (Rac+Rbc). Вычислять их общее сопротивление мы умеем (ответы на вопросы 3 и 4). Вычисляем сопротивления между точками A и C, B и C (2 и 3 строчки). Обратите внимание, что во всех формулах знаменатель одинаковый.
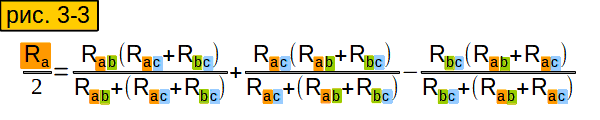
Теперь можно вычислить сопротивление отдельного луча (рис. 3-3). Формула получилась очень громоздкая, но мы её хорошенько подсократим.
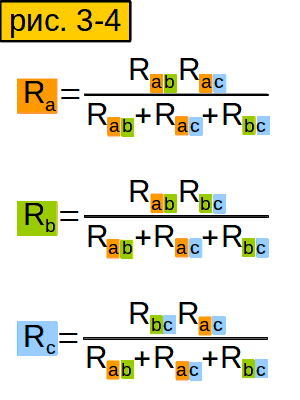
И получим вот такую стройную и изящную формулу (рис. 3-4, верхняя строчка). Аналогично вычисляем сопротивления других лучей звезды.
Сформулируйте своими словами формулу из рисунка 3-4, чтобы лучше её запомнить.
Чтобы найти сопротивление луча "звезды", надо умножить сопротивления сторон "треугольника", которые "прилегают" ("имеют ту же букву"), и разделить на сумму сопротивлений всех сторон "треугольника".
Иногда полезно делать обратное преобразование - "звезды" в "треугольник". Нельзя ли вычислить сопротивление стороны "треугольника" через сопротивления эквивалентной "звезды", используя формулы, которые мы уже вывели? Можно. Смотрим рисунок 3-4. Проделаем с формулами этого рисунка следующий трюк: попарно их перемножим и результаты сложим (смотрим рис. 4-1).
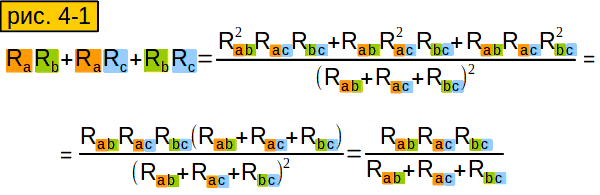
Затем результат разделим на верхнюю формулу рисунка 3-4. Получится у нас вот что: рисунок 4-2, третья сверху формула. Маленько её подсократим и получим нижнюю формулу. Как раз то, что нам надо!
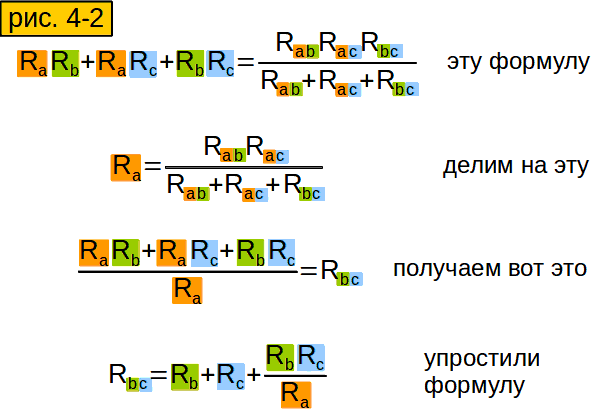
Сопротивления других сторон "треугольника" выводятся аналогично (рисунок 4-3).
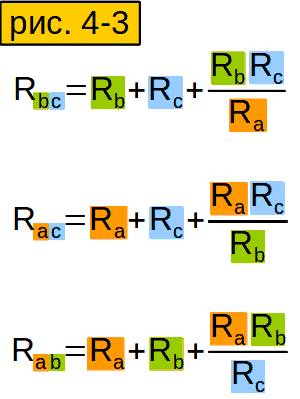
Сформулируйте своими словами формулу из рисунка 4-3, чтобы лучше её запомнить.
Чтобы найти сопротивление стороны "треугольника", надо сложить сопротивления соответствующих сторон "звезды" (у которых "те же буквы"), и ещё прибавить произведение тех же сторон "звезды", делёное на оставшуюся сторону.



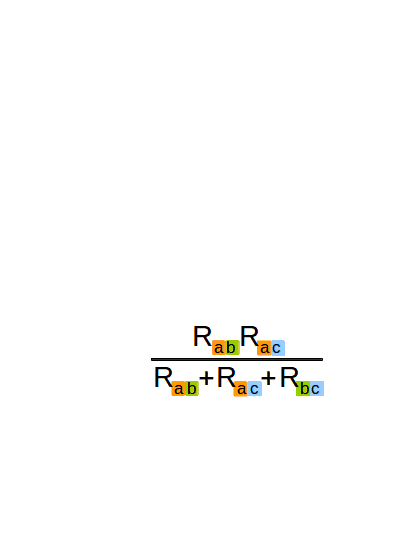

об ошибках сообщайте по адресу obuchmat@mail.ru